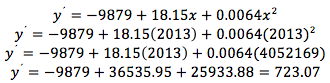---

Modelo de regresión de segundo orden

Este modelo se emplea cuando las tendencias del flujo de población y las hipótesis sobre su crecimiento anual indican que la población está disminuyendo paulatinamente; de esto resulta que su representación gráfica es la correspondiente a una parábola y no a una recta. Por lo tanto este modelo será de utilidad para hacer estimaciones cuando:

Las magnitudes de población que se verán reducidas por modificaciones contextuales relevantes (como una política rígida de acceso educativo), que iniciarán con una alta probabilidad en la tendencia histórica hasta la presente obtenida.

La fórmula utilizada en estos modelos es:

O bien la podemos escribir de la siguiente manera: Donde:



a,b,c=Son parámetros desconocidos que serán estimados
x= Valor en el cual se desea proyectar (Variable independiente)
y= Variable dependiente

Para estimar estos parámetros el procedimiento es muy similar al efectuado en la regresión de primer orden. Sin embargo, habrá de emplearse un procedimiento más laborioso para resolver los casos de este tipo de regresiones ya que esta resolución involucra a un conjunto de tres ecuaciones con tres incógnitas.

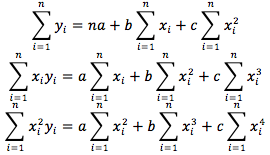
Si aplicamos el método de determinantes tenemos que:



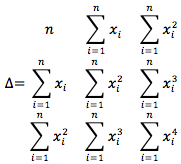
Entonces:

---

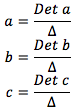
Ejemplo

Se sabe que la matricula de cierta universidad está disminuyendo drásticamente, debido a ciertas políticas que se han implementado y que tienen descontentos tanto a padres como alumnos. Se requiere estimar si sigue esta tendencia cuántos alumnos se inscribirán en el ciclo 2013.
Considera que se ha resuelto en Excel el conjunto de tres ecuaciones con tres incógnitas utilizando determinantes y se ha obtenido la siguiente ecuación:

Solución

Paso 1.Identificamos la variable dependiente y la variable independiente.

• La variable independiente en este caso son los años, por lo que le asignamos el valor de x
• La variable dependiente entonces le corresponde a la matricula que le corresponderá a y

Paso 2. Calculamos los datos faltantes para poder aplicar la fórmula.



Paso 3. Realizamos el cálculo de la población futura requerida, en este caso del 2013, entonces:

Con la formula que nos proporcionan realizamos el cálculo para el año indicado:

Por lo tanto el número estimado de matrícula para el año 2013 es de 723 alumnos, por lo que es urgente que las autoridades educativas planeen como remediar esta situación.